Converted Waves

Jika gelombang P atau S merambat melalui medium kemudian menghantam batas perlapisan, maka gelombang tersebut akan terkonversi menjadi gelombang yang lain. Gelombang yang terkonversi ini dinamakan converted waves.

Dalam dunia seismik eksplorasi (refleksi), dikenal beberapa jenis converted waves: Rpp, Rps, Rss dan Rsp. Rpp adalah gelombang P yang terkonversi menjadi gelombang P yang baru, Rps adalah gelombang P yang terkonversi menjadi gelombang S, Rss adalah gelombang S yang terkonversi menjadi gelombang S yang baru dan Rsp adalah gelombang S yang terkonversi menjadi gelombang P.

Gambar di bawah ini mengilustrasikan konversi gelombang P pada medium dengan kecepatan gelombang P (α), kecepatan gelombang S (β), dan densitas (ρ) yang menghasilkan gelombang Refleksi (R) dan gelombang Transmisi (T).

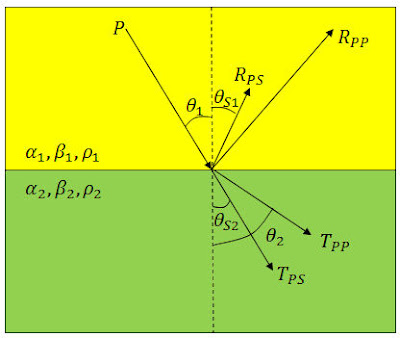Meskipun respon amplitudo converted waves dapat diturunkan dari Persamaan Zoeppritz, tetapi untuk kepraktisan komputasi, dilakukan pendekatan-pendekatan, diantaranya oleh Aki dan Richards (1980):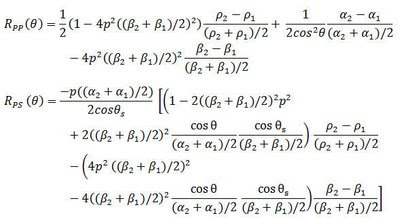

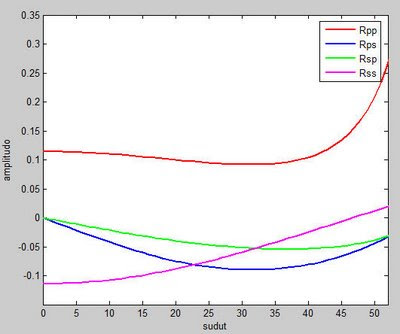
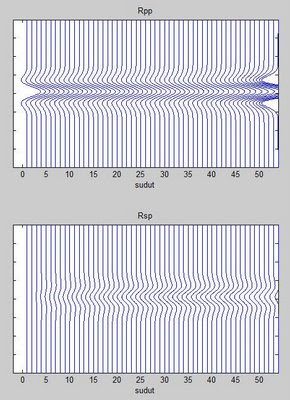
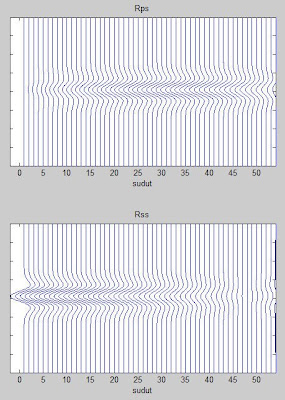Gambar di bawah ini menunjukkan kurva amplitudo terhadap sudut maupun respon seismiknya.

Gambar-gambar di atas diperoleh dengan menggunakan program dibawah ini:

%%%matlab scripts for converted waves simulation
%%%by Agus Abdullah, PhD
%%%prepared for ensiklopediseismik.blogspot.com
clear; clc
%%input parameters
alpha1=2000;
beta1=1000;
rho1=2.1;
alpha2=2400;
beta2=1200;
rho2=2.2;
tethap1=[0:53];
tethap2=180/pi*asin(((sin(tethap1*pi/180))./alpha1)*alpha2) ;
tethap=(tethap1+tethap2)./2;
tethas1=180/pi*asin(((sin(tethap1*pi/180))./alpha1)*beta1) ;
tethas2=180/pi*asin(((sin(tethas1*pi/180))./beta1)*beta2) ;
tethas=(tethas1+tethas2)./2;

alpha_av=(alpha2+alpha1)/2;
beta_av=(beta2+beta1)/2;
alpha_d=alpha2-alpha1;
beta_d=beta2-beta1;
rho_av=(rho2+rho1)/2;
rho_d=rho2-rho1;

p=sin(tethap1*pi/180)/alpha1; %%rays parameter p

Rpp=0.5*(1-(4*p.^2)*beta_av^2)*rho_d/rho_av+(1./(2*(cos(tethap*pi/180)).^2))*(alpha_d/alpha_av)-(4*p.^2)*(beta_av^2)*(beta_d/beta_av);
Rps=(-p*alpha_av)./(2*cos(tethas*pi/180)).*((1-2*beta_av.^2.*p.^2+2*beta_av.^2.*(cos(tethap*pi/180)/alpha_av).*(cos(tethas*pi/180)/beta_av))*(rho_d/rho_av)-(4.*p.^2*beta_av.^2-4*beta_av.^2.*(cos(tethap*pi/180)/alpha_av).*(cos(tethas*pi/180)/beta_av)).*(beta_d./beta_av));
Rsp=(cos(tethas*pi/180)./alpha_av).*(beta_av./cos(tethap*pi/180)).*Rps;
Rss=-0.5*(1-4*p.^2.*beta_av.^2).*(rho_d/rho_av)-(1./(2*cos(tethas*pi/180).^2)-4.*p.^2.*beta_av.^2).*(beta_d./beta_av);

plot(tethap1,Rpp,'r',tethap1,Rps,'b',tethap1,Rsp,'g',tethap1,Rss,'m','linewidth',2)
xlabel('sudut')
ylabel('amplitudo')
axis([0,52,-0.15,0.35])
legend('Rpp','Rps','Rsp','Rss')
%%%ricker wavelet parameters
t=[-250:250];
dt=0.0005;
to=0;
f=25;
rw=(1-2*(pi*f*dt*(t-to)).^2)./exp((pi*f*dt*(t-to)).^2); %%%ricker wavelet generator
matrix=repmat(eye(54),1,1)*0;

%%reflectivity calculation
Rpp_m=[matrix;Rpp;matrix];
Rps_m=[matrix;Rps;matrix];
Rsp_m=[matrix;Rsp;matrix];
Rss_m=[matrix;Rss;matrix];

figure
for i=1:54
tracepp{i}=conv(Rpp_m(:,i),rw);
traceps{i}=conv(Rps_m(:,i),rw);
tracesp{i}=conv(Rsp_m(:,i),rw);
tracess{i}=conv(Rss_m(:,i),rw);

subplot(2,2,1)
plot(25*tracepp{i}+i,[1:length(tracepp{i})]); hold on
xlabel('sudut')
title('Rpp')
axis([-2,54,100,500])
subplot(2,2,2)
plot(25*traceps{i}+i,[1:length(traceps{i})]); hold on
xlabel('sudut')
title('Rps')
axis([-2,54,100,500])
subplot(2,2,3)
plot(25*tracesp{i}+i,[1:length(tracesp{i})]); hold on
xlabel('sudut')
title('Rsp')
axis([-2,54,100,500])
subplot(2,2,4)
plot(25*tracess{i}+i,[1:length(tracess{i})]); hold on
xlabel('sudut')
title('Rss')
axis([-2,54,100,500])
end
clear; clc